DIMENSI TIGA - KLS 12 MATEMATIKA WAJIB

DIMENSI TIGA

KOMPETENSI DASAR

3.1. Mendeskripsikan jarak dalam ruang   

               ( antara titik, titik ke garis, dan titik ke bidang )  

        4.1. Menentukan jarak dalam ruang  

               ( antara titik, titik ke garis, dan titik ke bidang )

                                                                        

Daftar Isi  

1. Kedudukan Titik, Garis, dan Bidang dalam Dimensi Tiga

2. Jarak titik, garis dan bidang

3. Sudut, garis dan bidang

https://images.app.goo.gl/nwGBVs6cdijF6U5o9

                                           

Kedudukan Titik, Garis, dan Bidang dalam Dimensi Tiga

Dimensi tiga terbentuk dari 3 elemen yaitu titik, garis, dan bidang. Titik adalah lukisan tanda noktah yang dibubuhi nama menggunakan huruf kapital. Suatu titik tidak memiliki besaran dan tidak berdimensi.  Garis adalah himpunan titik-titik yang hanya memiliki ukuran panjang dan berdimensi satu. Sedangkan bidang adalah himpunan titik-titik yang memiliki ukuran panjang dan luas, sehingga dikatakan berdimensi dua. Bidang adalah luasan (bidang datar), dan hanya dapat dibentuk dari : 

1. Tiga titik berbeda
2. Satu titik dan satu garis
3. Dua garis yang berpotongan atau sejajar. 

Contoh titik, garis, dan bidang digambarkan di bawah ini : 

Suatu titik, garis, ataupun bidang memiliki suatu posisi atau kedudukannya satu sama lain. Kedudukan ini mempunyai syarat-syarat khusus yaitu sebagai berikut : 

Kedudukan titik terhadap garis

a. Titik terletak pada garis

Titik berada pada garis karena garis itu melalui titik. Contohnya titik A, P, dan titik B pada gambar 2.

b. Titik berada di luar garis

Titik berada di luar garis karena garis itu tidak melalui titik. Contohnya titik Q. 

Kedudukan titik terhadap bidang

Titik berada pada bidang terjadi karena :

1. Bidang melalui titik.
2. Titik berada pada garis yang terletak pada bidang itu.

Contohnya titik P

Titik berada di luar bidang

Titik berada di luar bidang terjadi karena :

1. Bidang tidak melalui titik
2. Titik tidak berada pada garis yang berada pada bidang itu. 

Contohnya titik Q

Kedudukan garis terhadap bidang adalah sebagai berikut : 

1. Garis berada terletak pada bidang contohnya garis AB,AC, dll (gambar 4). Garis berada pada bidang karena ada dua titik yang dilalui garis pada bidang itu.
2. Garis memotong atau menembus bidang yaitu contohnya garis PQ. Garis menembus/memotong bidang karena ada satu titik yang dilalui garis pada bidang itu (titik tembus).
3. Garis sejajar dengan bidang contohnya garis RS. Garis sejajar dengan bidang karena garis itu sejajar dengan salah satu garis pada bidang itu atau tidak memiliki satupun titik persekutuan. 

Kedudukan Bidang terhadap Bidang lain

a. Dua bidang yang saling sejajar. 

Dua bidang sejajar apabila tidak ada satupun garis berpotongan bidang dari kedua bidang. 

b. Dua bidang saling berpotongan

Dua bidang berpotongan apabila terdapat garis perpotongan bidang, yaitu garis persekutuan yang merupakan bagian dari kedua bidang. 

c. Dua bidang saling berimpit

Dua bidang saling berimpit ( α, β). Apabila setiap titik yang terletak pada bidang α juga terletak pada bidang β atau setiap titik yang terletak pada bidang β juga terletak pada bidang α.

Kedudukan titik, garis dan bidang memiliki suatu aksioma. Aksioma adalah sebuah pernyataan dimana pernyataan yang kita terima sebagai suatu kebenaran dan bersifat umum. Tanpa perlu adanya pembuktian dari kita sendiri. Aksioma terhadap kedudukan garis, dan bidang adalah sebagai berikut : 

1. Apabila dua buah bidang berpotongan tegak lurus, maka seluruh garis dari bidang 1 terhadap bidang 2 juga tegak lurus. 
2. Hasil perpotongan dua bidang adalah garis, sedangkan hasil perpotongan tiga bidang dapat berupa garis atau titik. 

Proyeksi Titik dan Garis Pada Bidang

Proyeksi adalah proses penjatuhan (pemindahan) titik dan garis pada suatu bidang. Proyeksi dapat disebut juga dengan pencerminan. Proyeksi dilakukan dengan cara menjatuhkan titik atau titik tersebut pada garis tegak lurus terhadap bidang, dan biasanya dilambangkan dengan tanda aksen (‘). Berikut di bawah ini adalah bentuk-bentuk proyeksi titik atau garis ke suatu bidang.

Jarak dari Titik ke Titik, Titik ke Garis, dan Titik ke Bidang

Jarak adalah panjang ruas garis penghubung kedua bangun itu yang terpendek dan bernilai positif. 

a. Jarak antara titik dan titik

Jarak antara titik A dan titik B adalah panjang ruas garis AB.

b. Jarak antara titik dan garis

Jarak antara titik A dan garis g (titik A terletak di luar garis g) adalah panjang ruas garis AA’, dengan titik A’ merupakan proyeksi titik A pada garis g. Dengan perkataan lain jarak antara titik A dan garis g ditentukan dengan cara menarik garis dari titik A tegak lurus garis g sehingga memotong garis g dititik A’, maka garis AA’ adalah jarak antara titik A dan garis g. (lihat gambar 11 (a) ).

Jika garis g terletak pada suatu bidang dan titik A berada di luar bidang tersebut, maka untuk menentukan jarak antara titik A dan garis g ditempuh dengan membuat garis AB yang tegak lurus bidang, kemudian tariklah garis BC yang tegak lurus garis g, sehingga diperoleh panjang ruas garis AC yang merupakan jarak antara titik A dan garis g. (lihat gambar 11 (b) ). 

c. Jarak antara titik dan bidang

Jarak antara titik A dan bidang α adalah panjang ruas garis AA’. Dengan titik A’ merupakan proyeksi titik A pada bidang α  .

Karena AA’  ⊥ a dan AA’   b   maka hasilnya adalah AA’    bidang α

Jarak Dua Garis Sejajar, Jarak Garis dan Bidang Yang Sejajar, Jarak Dua Bidang Sejajar

a. Jarak Dua Garis Sejajar

Jarak antara garis g dan h yang sejajar adalah garis AB, dengan titik A adalah sebarang titik pada garis g dan titik B merupakan proyeksi titik A pada garis h. 

b. Jarak antara garis dan bidang yang sejajar

Jarak antara garis g dan bidang α = panjang ruas garis AB ( AB tegak lurus bidang α dan garis g). 

c. Jarak dua bidang yang saling sejajar

Bidang α sejajar dengan bidang β maka jarak kedua bidang = panjang ruas garis AB ( AB tegak lurus dengan kedua bidang). 

SOAL DAN PEMBAHASAN DIMENSI TIGA

Soal Nomor 1

Diketahui kubus $ABCD.EFGH$ dengan panjang rusuk $2a$ cm. Panjang ruas garis $HB$ adalah $\cdots \cdot$
A. $(2a\sqrt{3}–a\sqrt{2})\text{cm}$       D. $2a\sqrt{2}\text{cm}$
B. $a\sqrt{2}\text{cm}$                   E. $2a\sqrt{3}\text{cm}$
C. $a\sqrt{3}\text{cm}$

Pembahasan

Perhatikan sketsa gambar berikut.

Pertama, perhatikan segitiga $ABD$ (siku-siku di $A$). Panjang $BD$ dapat ditentukan dengan rumus Pythagoras, yaitu
$\begin{array}{cc}BD& =\sqrt{A{B}^2+A{D}^2}\\ & =\sqrt{(2a{)}^2+(2a{)}^2}\\ & =\sqrt{8a^2}=2a\sqrt{2}\text{cm}\end{array}$
Sekarang, perhatikan segitiga $BDH$ (siku-siku di $D$). Panjang $HB$ juga dapat ditentukan dengan rumus Pythagoras, yaitu
$\begin{array}{cc}HB& =\sqrt{B{D}^2+D{H}^2}\\ & =\sqrt{(2a\sqrt{2}{)}^2+(2a{)}^2}\\ & =\sqrt{8a^2+4a^2}\\ & =\sqrt{12a^2}=2a\sqrt{3}\text{cm}\end{array}$
Jadi, panjang ruas garis $HB$ adalah $2a\sqrt{3}\text{cm}$
(Jawaban E)

Soal Nomor 2
Diketahui kubus $ABCD.EFGH$ dengan panjang rusuk $8$ cm. Jarak titik $B$ ke garis $HC$ adalah $\cdots \cdot$
A. $12\sqrt{2}\text{cm}$         D. $8\text{cm}$
B. $8\sqrt{5}\text{cm}$           E. $4\sqrt{6}\text{cm}$
C. $8\sqrt{3}\text{cm}$

PEMBAHASAN

Perhatikan sketsa gambar berikut.

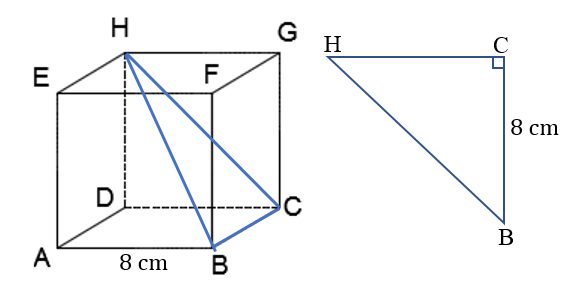
Jarak titik $B$ ke $HC$ sama dengan jarak titik $B$ ke $C$. Perhatikan bahwa $BC$ merupakan rusuk kubus, sehingga panjang $BC=8\text{cm}$. 
Jadi, jarak titik $B$ ke garis $HC$ adalah $8\text{cm}$
(Jawaban D)

Soal Nomor 3
Diketahui kubus $ABCD.EFGH$ dengan panjang rusuk $6$ cm. Jarak antara titik $B$ dan $EG$ adalah $\cdots \cdot$
A. $3\sqrt{6}\text{cm}$            D. $6\sqrt{6}\text{cm}$
B. $4\sqrt{6}\text{cm}$            E. $7\sqrt{6}\text{cm}$
C. $5\sqrt{6}\text{cm}$

Pembahasan

Perhatikan sketsa gambar berikut.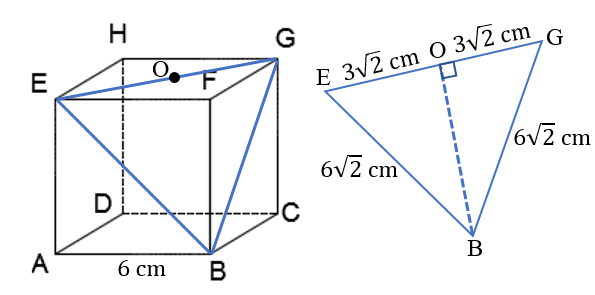

Pada segitiga $BEG$, diketahui $BE,EG$, dan $BG$ semuanya merupakan diagonal bidang kubus, sehingga segitiga $BEG$ merupakan segitiga sama sisi dengan panjang $BE=EG=BG=6\sqrt{2}\text{cm}$. Untuk itu, jarak $B$ ke $EG$ adalah jarak $B$ ke $O$ di mana $O$ titik tengah $EG$. 
Sekarang tinjau segitiga siku-siku $BOG$. Diketahui: $OG=\frac{1}{2}EG=\frac{1}{2}\left(6\sqrt{2}\right)=3\sqrt{2}\text{cm}$ dan $BG=6\sqrt{2}\text{cm}$
Panjang $BO$ dapat ditentukan dengan Teorema Pythagoras. 
$\begin{array}{cc}BO& =\sqrt{B{G}^2-O{G}^2}\\ & =\sqrt{(6\sqrt{2}{)}^2-(3\sqrt{2}{)}^2}\\ & =\sqrt{72-18}\\ & =\sqrt{54}=3\sqrt{6}\text{cm}\end{array}$
Jadi, jarak $B$ ke $EG$ adalah $3\sqrt{6}\text{cm}$
(Jawaban A)

Soal Nomor 4
Diketahui kubus $ABCD.EFGH$ dengan rusuk $8\text{cm}$. $M$ adalah titik tengah $EH$. Jarak titik $M$ ke garis $AG$ sama dengan $\cdots \cdot$
A. $4\sqrt{6}\text{cm}$               D. $4\sqrt{2}\text{cm}$ 
B. $4\sqrt{5}\text{cm}$               E. $4\text{cm}$
C. $4\sqrt{3}\text{cm}$ 

Pembahasan

Perhatikan sketsa gambar berikut.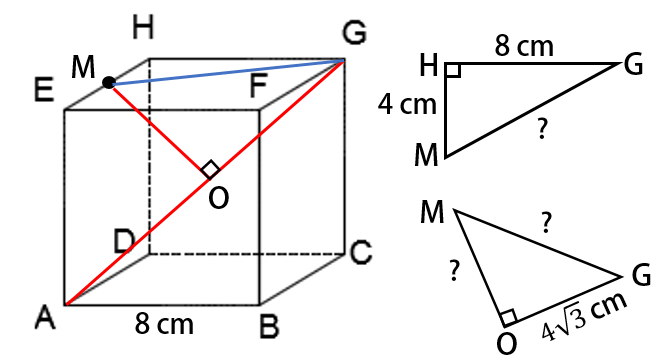

Misalkan titik $O$ merupakan proyeksi titik $M$ pada garis $AG$. Titik $O$ tepat di tengah $AG$ karena panjang $MA$ dan $MG$ sama.
Pertama, perhatikan segitiga siku-siku $MHG$.
Diketahui $HG=8\text{cm}$ dan $MH=4\text{cm}$ (setengah dari panjang rusuk kubus). Dengan Teorema Pythagoras, diperoleh
$\begin{array}{cc}MG& =\sqrt{H{G}^2+M{H}^2}\\ & =\sqrt{8^2+4^2}\\ & =\sqrt{64+16}=\sqrt{80}=4\sqrt{5}\text{cm}\end{array}$
Sekarang, tinjau segitiga siku-siku $MOG$. Diketahui $OG=4\sqrt{3}\text{cm}$ (setengah dari panjang diagonal ruang kubus) dan $MG=4\sqrt{5}\text{cm}$. Dengan Teorema Pythagoras, diperoleh
$\begin{array}{cc}MO& =\sqrt{M{G}^2-O{G}^2}\\ & =\sqrt{(4\sqrt{5}{)}^2-(4\sqrt{3}{)}^2}\\ & =\sqrt{80-48}=\sqrt{32}=4\sqrt{2}\text{cm}\end{array}$
Jadi, jarak titik $M$ ke garis $AG$ sama dengan $4\sqrt{2}\text{cm}$
(Jawaban D)

Soal Nomor 5
Panjang rusuk kubus $ABCD.EFGH$ adalah $12\text{cm}$. Jika $P$ titik tengah $CG$, maka jarak titik $P$ ke garis $HB$ adalah $\cdots \cdot$
A. $8\sqrt{5}\text{cm}$              D. $6\sqrt{2}\text{cm}$ 
B. $6\sqrt{5}\text{cm}$              E. $6\text{cm}$
C. $6\sqrt{3}\text{cm}$ 

Pembahasan

Perhatikan sketsa gambar berikut.

Misalkan $O$ merupakan proyeksi titik $P$ ke garis $HB$. Titik $O$ berada di tengah garis $HB$ karena $PB=PH$.
Pertama-tama, perhatikan dulu segitiga siku-siku $BCP$.
Diketahui bahwa $BC=12\text{cm}$ dan $CP=6\text{cm}$, sehingga dengan menggunakan Teorema Pythagoras, diperoleh
$\begin{array}{cc}BP& =\sqrt{B{C}^2+C{P}^2}\\ & =\sqrt{{12}^2+6^2}\\ & =\sqrt{144+36}=\sqrt{180}=6\sqrt{5}\text{cm}\end{array}$
$HB$ merupakan diagonal ruang kubus, dan karena panjang rusuknya $s=12\text{cm}$, maka $HB=s\sqrt{3}=12\sqrt{3}\text{cm}$. Ini berarti $PH=\frac{1}{2}\left(12\sqrt{3}\right)=6\sqrt{3}=\sqrt{108}\text{cm}$
Selanjutnya, perhatikan segitiga siku-siku $BOP$.
Panjang $OP$ merupakan jarak titik $P$ ke garis $HB$. Dengan menggunakan Teorema Pythagoras kembali, diperoleh
$\begin{array}{cc}OP& =\sqrt{B{P}^2-O{B}^2}\\ & =\sqrt{180-108}\\ & =\sqrt{72}=6\sqrt{2}\text{cm}\end{array}$
Jadi, jarak titik $P$ dengan garis $HB$ adalah $6\sqrt{2}\text{cm}$
(Jawaban D)

Soal Nomor 6
Diketahui kubus $ABCD.EFGH$ dengan panjang rusuk $a$ cm. Jarak titik $E$ ke bidang diagonal $BDHF$ adalah $\cdots \cdot$ 
A. $\frac{1}{2}a\sqrt{3}\text{cm}$           D. $\frac{1}{2}a\text{cm}$
B. $\frac{1}{2}a\sqrt{2}\text{cm}$           E. $\frac{1}{4}a\text{cm}$
C. $\frac{1}{4}a\sqrt{2}\text{cm}$

Pembahasan

Perhatikan sketsa gambar berikut.

Jarak titik $E$ ke bidang diagonal $BDHF$ sama dengan jarak titik $E$ ke titik tengah diagonal $HF$. Misalkan $O$ titik tengah diagonal $HF$. $EG$ merupakan diagonal bidang dengan panjang $a\sqrt{2}\text{cm}$.
Perhatikan bahwa panjang $EO$ merupakan setengah dari panjang diagonal $EG$, sehingga
$EO=\frac{1}{2}\left(a\sqrt{2}\right)=\frac{1}{2}a\sqrt{2}\text{cm}$ 
Jadi, jarak titik $E$ ke bidang diagonal $BDHF$ adalah $\frac{1}{2}a\sqrt{2}\text{cm}$
(Jawaban B)